Deep Learning Is Better Than Linear Regression
A hype-free introduction for the curmudgeonly data scientist
Every day, millions of brilliant people run linear regressions.
Maybe you are one of them. Maybe you are a social scientist, estimating population effects from demographic characteristics. Maybe you are a stock trader, predicting price movements from market conditions. Maybe you are a business owner, predicting future demand based on consumption trends. Maybe you are a doctor, estimating medication efficacy based on patient attributes. Or maybe you’ve got some other good reason to be running linear regressions. If you’re reading this essay, I’m going to assume that you do.
You probably like your linear regressions a lot. And for good reason: linear regression is a great technique! It’s simple to implement, possesses a tantalizingly tractable runtime, and comes with all sorts of theoretical guarantees. Best of all, it’s as reliable and battle-tested as they come. Linear regression dates back to Gauss in the early 1800s (and possibly earlier), and since it is such a deep and generic technique, it has proven its worth in all sorts of different areas of mathematics and physics. Hell, linear regression put a man on the moon. You really can’t go wrong with linear regression.
But a stable relationship is a boring one. Over the years, you’ve probably been tempted away from your stodgy-but-reliable linear regression by a shiny new statistical technique on at least one occasion. “More accuracy!” promised the academic statistician, with a glimmer in his eye. “State-of-the-art performance!” Enthralled by these claims, you dutifully waded through the morass of difficult-to-parse math, gnarly code, and questionable assumptions in order to put together a functional implementation of this algorithm on your task of interest. But at the end of the road lay only disappointment. This shiny new algorithm did not provide the gains that were promised, and maybe even made things worse! Frustrated, you switched back to good old linear regression and swore never to have your heart broken again.
I fully empathize with this mindset, I really do. Most “progress” in machine learning, even now, is closer to self-interested academic paper-pushing than to genuine algorithmic progress. It’s tempting to fully immerse yourself in cynicism, to stick only to linear regression and dismiss alternatives. But a comprehensive dismissal means blinding yourself to the rare moments of actual, meaningful progress. And today, I’m going to try to convince you that such a moment has come to pass. Over the last decade, a real paradigm shift has occurred.
The heyday of linear regression has come and gone. Ours is the era of non-linear regression: deep learning.
A Proper Comparison
You’ve probably heard of deep learning. Over the past few years, it’s been an unavoidable topic for anybody in an even remotely-tech-adjacent circle. Beating human pros at Go and Starcraft and Dota, guiding self-driving Teslas, translating languages, generating images, writing code…it’s clearly capable of doing some pretty cool things. More recently, everybody seems to be getting excited about conversational deep learning agents like ChatGPT. But – you may be thinking – are these achievements really all that useful? Many of these examples seem a bit…whimsical. Sure, deep learning can be used to play a child’s video game, but is it useful for your serious real-world task?
In this essay, I aim to give a proper empirical justification for deep learning. I’m not even going to explain what deep learning is – if you’re interested in that content, there are plenty of introductions I can point you to. I’m only here to show you what it does. Using a simple didactic example task, I’ll demonstrate empirically what outcomes one can expect from using deep learning as a straightforward drop-in replacement for linear regression.1
A Linear Regression Warmup
Let’s start by taking a look at our first task. Here’s what we know. There are 256 input features, each taking a value between -1 and 1. The output is a number between 0 and 1, and may be noisy. There are 1,000 datapoints in the training set (for now), and 40,000 in the test set.2 In classic linear regression style, we’re going to minimize the average squared-error of the predictions. One slightly unusual thing I’ll be doing is using stochastic gradient descent to approximately minimize the error instead of finding a closed-form solution. I do this because gradient descent is a much faster algorithm when the dataset is large -- and I will be enlarging the dataset soon. We’re going to be measuring performance using the out-of-sample R-squared, although note that on the figures, I plot (1 - R-squared) instead, so lower is better.
To begin, let’s see how a linear regression performs.

Not bad; it’s clearly learned something. Note however that the in-sample performance is quite a bit higher than the out-of-sample performance. Also, beyond a certain point, training longer causes performance to degrade. This means our model is overfitting the training data. One classic way to fix overfitting is to add some L2 regularization. Let’s try it out, and do a small sweep over values for the regularizer weight.
L2 regularization seems to work as advertised: it decreases the in-sample performance, but mitigates the overfitting issue, and overall improves performance. We can visualize the impact of the regularization weight hyperparameter tuning by plotting the final performance of each run.
The out-of-sample curve has a U-shape, which tells us that tuning is important. We see that the optimal value for the regularizer seems to be around 0.5, and that this lets us reach an error of 62%.
Not bad, but still leaves a lot to be desired. Even with optimally-tuned regularization, the train-test gap is still massive, and out-of-sample performance only improved by about 15%. Also, the fact that it needs to be tuned is not ideal (repeated runs can get expensive).
So L2 regularization isn’t a great solution here, let’s remove it and try something else.
A second possible fix to overfitting is to just find more data. What happens when we increase the size of the training dataset? Let’s try the same experiment, but with 10,000 data points.
Once again, we see that this approach fixes overfitting and improves performance on out-of-sample data. It also shrinks the train-test gap significantly.
Acquiring all that new data might be expensive. How many data points would it have taken to get this result? Once again, let’s measure the impact of this modification by re-running the whole experiment at various dataset sizes and plotting the final performance.
We can see that for small datasets, we have a big train-test gap (indicating overfitting), but as the dataset gets larger, this vanishes: the train set gets harder to fit, and the resulting model generalizes better to the out-of-sample data, so the two lines come together. At first, increasing data gives us a large improvement in out-of-sample performance, but the marginal benefit of each extra datapoint falls off quickly. At some point, we can’t get much more improvement from adding data.
Overall, this approach seems better than L2 regularization, albeit potentially more expensive. The performance curve shows a smooth decrease, not a U-shape, so no tuning is necessary: adding more data always helps. Also, it reaches a slightly better final performance of 58% error, down from 61% with optimal regularization.
But now that the overfitting is fixed, where do we go from here? Can we continue to improve performance further?
The main option left in our toolkit is feature engineering. We are training a linear model, which means that our training process is only capable of capturing linear relationships between the inputs and outputs. Maybe the features we are feeding in aren’t linearly predictive of the outcome, but some other features would be.
Let’s try adding in new features corresponding to the squared value of each of our original features. The resulting model has twice as many features, meaning it has twice as many parameters, too. Does this help? Let’s compare, again looking at various dataset sizes.
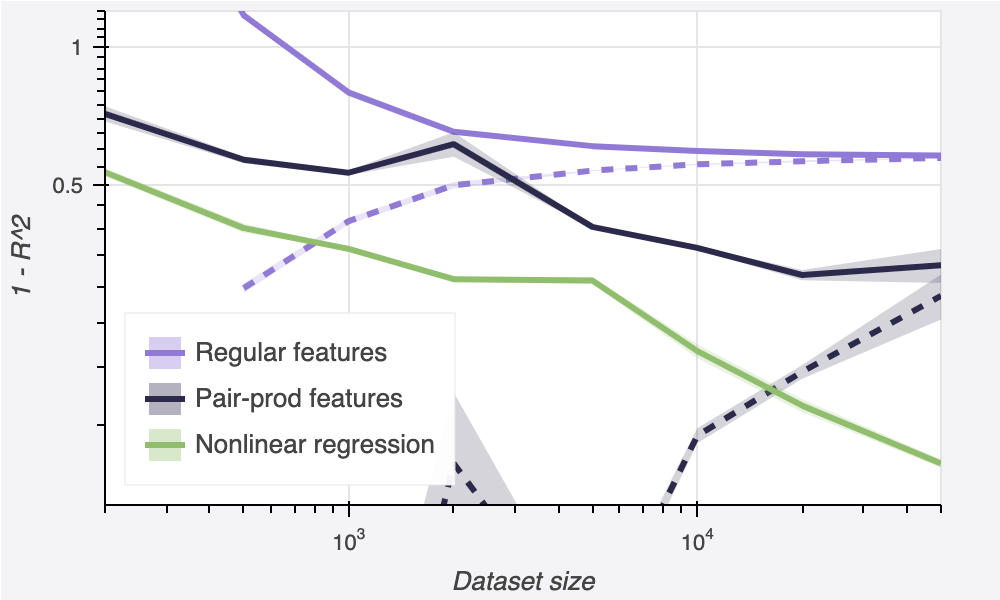
As you might have expected, we see a modest improvement in performance at the largest dataset sizes, as well as a modest increase in overfitting on small data. We’ve successfully improved our out-of-sample performance, too — as long as we have at least 2,500 data points. Overall, this pushes us down to about 52% error.
Let’s keep going. How about we add the rest of the pair-wise multiplicative features? That is, we add features for
This brings us up to a whopping 33,152 features.
Here, the effect of the feature engineering becomes more dramatic. The out-of-sample performance is consistently improved, at all train-set sizes. Surprisingly, this is true even on the smallest datasets, where we might have expected to see additional overfitting. (Take note of this! It is our first clue that the conventional wisdom, which is that increasing the size of the model causes overfitting, may not be completely correct.) We are able to reduce our error all the way down to 33%, a massive improvement.
Where should we go from here? We could try to add even more features, maybe including some esoteric functions, or more higher-order polynomial terms. This would probably improve performance a bit further, but require a decent amount of work to implement, since we’d have to spend some time brainstorming features and trying them out. I’m sure the experienced linear regressors in my audience will have some suggestions. In any case, let’s take a break from linear regression for now to see how deep learning – non-linear regression – would handle this same problem.
Learning Deeply And Cheaply
I know I promised that this post wouldn’t be a deep learning explainer, but I want to give just the briefest description of how it works to give some context to these experiments. The simplest instantiation of deep learning (which is the one I’m using here) basically consists of a bunch of parameterized linear transformations applied in sequence. In between each one, a pointwise nonlinearity is applied; essentially, this yields a set of new “intermediate features” that are fed into the next linear transformation. Each of these intermediate transformations is called a layer. The final layer is just a regular linear regression, mapping the last set of intermediate features to an output number. Finally, we use gradient descent to minimize the squared error between that prediction and the target, just as we did for linear regression.
One important detail to be aware of is how deep learning decouples model size from feature count. If you are used to thinking about linear regression, your conception of the “size” of the model is probably just the number of input features, since the model always has one parameter per input feature. But in deep learning, this is no longer the case, because each of the intermediate features has its own set of parameters. This means we can increase the size of a deep learning model without increasing the number of input features, by increasing the number of intermediate features.
To describe a deep learning model, we need to specify its layout. The small network we will start with will have shape [32,32,16], which means it has 3 layers, with 32 intermediate features after the first layer, 32 new intermediate features after the second layer, and 16 intermediate features after the third layer.
Let’s take this basic deep learning model and compare it to linear regression on the original dataset, which contains inputs with 256 features and holds 1,000 datapoints.
We immediately see the impact of this change. Despite only having 100 input features, the nonlinear regression model qualitatively behaves like it has many more: it has a large train-test gap, near-perfect performance on the train set, and good out-of-sample performance.
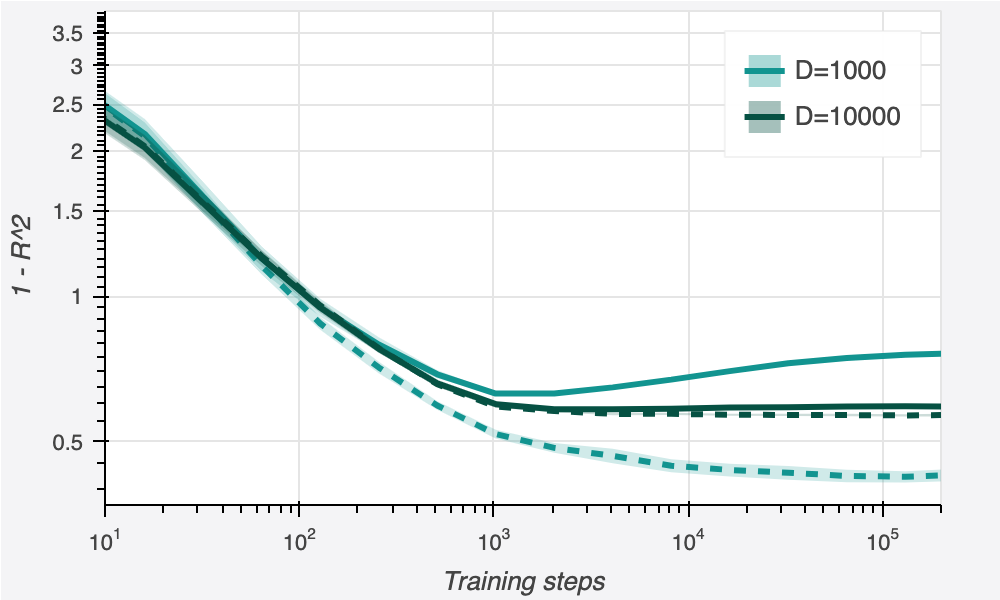
Nonlinear regression meaningfully outperforms linear regression throughout training. Still, at around 250 steps of training, we do see something that looks a bit like overfitting, as out-of-sample performance begins to degrade somewhat. But after 2000 steps of training, this trend reverses! By 200,000 steps of training, performance has not only fully recovered, but even improved further. This is our second clue that there is more to “overfitting” than the usual story.
Now, just as we did for linear regression, let’s see how this algorithm fares on various sizes of dataset. We will compare both to linear regression with basic features, and to the feature-engineered version (the best model we’ve seen so far).
We see a dramatic gap. Nonlinear regression reaches performance better than any of the linear models we looked at, for all sizes of dataset. Our best-performing model has dropped all the way down to 12% error. This is already a clear win, but we’re only scratching the surface of the power of deep learning. Once again: let’s push it further.
When we did linear regression, our next step at this point was to increase the feature space. But for non-linear regression, this is not needed. Any useful nonlinear features that we could engineer into the feature space can just be learned by the intermediate features instead, provided that the network is large enough. So instead of engineering new features, we can just increase the size of our network. Let’s re-run that same experiment using larger models: a medium-sized model of [64,64,32], a large model of [128, 128, 64, 64], huge [256, 256, 256, 256], and enormous [512, 512, 512, 512].
We see performance tends to increase as we scale up the model, and that the magnitude of this effect grows as the dataset size grows larger. On the largest dataset, simply scaling up the model cuts error almost in half, from 12% all the way down to 7%.
Which Approach Scales Better?
Let’s recap what we’ve seen so far. Firstly, that linear and nonlinear regression have a lot in common. They share the basic framework, the loss function, and can be optimized with the same algorithm. Both approaches have the potential to overfit, and this tendency can be mitigated by providing lots of data. And each has a natural lever by which to increase their power, which can sometimes cause overfitting, but otherwise improves performance.
The crucial distinction, though, is in how the power of the model is increased. For linear regression, we increase the power by augmenting the feature space, carefully choosing the new features to include. For deep learning, we increase the size by giving the network more intermediate features to work with — in practice, this comes down to mindlessly increasing some hyperparameters. It’s not immediately obvious, but you should view this as a huge point in the favor of deep learning, and it is important to understand why.
Switching from linear to nonlinear regression represents a switch from manually-engineered features into features “discovered” by gradient descent. The bitter lesson of the last few decades is that you and I, as two humans, are not as good at identifying useful features as gradient descent. Deep learning frees us all from the burden of our own inadequacy by allowing the model to choose for itself which complex nonlinear features to include.
Note that in this example, even a very small deep learning model (with only ~9,800 parameters) worked better than the 33,152-feature linear model. So it’s not just a matter of parameter count. The intermediate features learned by the small deep learning model were clearly better than the ones I added manually. There are a couple caveats to this; I didn’t utilize any domain knowledge, my choice of features was naive, I didn’t push it very hard. But here’s the thing: I didn’t push deep learning very hard, either. I didn’t have to, and that’s the whole point. In deep learning, gradient descent did the work for me. As tasks get more challenging, the amount of work I need to put in to find comparably-useful features grows, and it soon becomes completely intractable for any human to design features as well as a neural network can discover them.
I want to state this one more time for emphasis: gradient descent is better than you at finding good features. Yes, I’m talking to *you*, Mr. Domain Expert. Yes, I’m aware that you have a PhD in this domain, and that you have spent your whole career identifying good features for ML models, and that you have a long resume of working on elite teams where only the best feature-identifiers are employed. But you’ll soon need to face the reality of the situation: when compared against the features learned by deep neural networks, your best efforts will inevitably fall short. A bitter lesson indeed.
Resource Woes
You probably have a big objection to this line of thinking. We’ve seen that deep learning can discover features, yes. But doing so seems to require a lot of data. In this essay, I’ve handwaved that away, because I have lots of data available for this toy task. But what if in the real world, you don’t have so much?
This is a totally understandable concern. All the feature-learning abilities in the world are useless if there isn’t enough data to learn them from. But things are not quite so dire as they may initially seem, thanks to some surprising and unintuitive properties of deep learning. This is where things may start to get a little funky: nonlinear regression, for all its similarities to its linear counterpart, is in some ways qualitatively completely different.
Overfitting Is Not What You Think
When it comes to deep learning, the elephant in the room is overfitting.

Thus far, I’ve paid lip service to the conventional wisdom on overfitting. The standard intuition is that if a model is sufficiently large, the learning procedure will simply memorize the training data, resulting in a function that is useless for out-of-sample predictions. Classic results in learning theory lend theoretical rigor to this intuition, by proving that the gap between in-sample error and out-of-sample error is guaranteed to be smaller than the complexity of the model (as measured by the so-called “VC dimension”). These led people to believe that the best models to use were the simple ones.
But as we have already begun to see, there is a more to the story.
Let’s take a look at the same data from before — where we trained deep learning models of various sizes — but visualized differently. Now, I’ll put the model size on the x-axis, and we can look at how performance on a particular dataset changes as we increase the model.
Take a close look at these curves. They may not look how you’d have predicted. What we would naïvely expect to see is, as the model gets larger, overfitting increases, and held-out performance drops. We maybe see this happen a little at intermediate dataset sizes, but in general, there is not much evidence of this trend. No, it seems that for this task, increasing the size of the model more-or-less always increases performance. In other words: we can make our models larger without worrying about overfitting.
If you studied machine learning between the years of 1990 - 2012, this claim is probably surprising. Indeed, I often find it hard to believe myself. But this is not a cherry-picked task; this property has been validated empirically in many domains. In the limits of dataset size and compute, models trained by gradient descent seem to monotonically improve with scale. It’s not completely clear, yet, why this is the case; the theory has not yet been developed to explain these empirical findings. Likely, the answer relies on a complex relationship between the implicit preferences of gradient descent, the structure in popular neural network architectures, and the fact that our datasets are constructed to include naturally-occurring patterns.
So why, then, do we sometimes what looks like overfitting? The modern understanding is that deep learning models exhibit double descent. There are two3 training regimes, with different behavior and tradeoffs in each. When the model is underparameterized, meaning that it has trouble fitting the dataset, your familiar intuitions still hold: as we make the model size larger, out-of-sample performance eventually starts to decay. When the model has just barely enough parameters to fit all the training data, at the “interpolation threshold”, its out-of-sample performance is at its worst. But if we keep increasing the power of the model beyond this point, performance once again begins to improve.

Intuitively, here’s how I interpret these properties. Deep learning models are always trying their hardest to explain as much of the training set as possible. If they are very small, they won’t be able to do a great job, and will just learn some general trends that somewhat explain it — and these high-level explanations will often carry over out-of-sample. Conversely, if they are very large, they will learn a beautiful, elegant explanation that not only fully explains all the training data, but actually captures its true patterns, leading to good performance on the whole space, including many out-of-sample datapoints. However, if the model has just barely enough parameters to explain the whole dataset (i.e. sits right at the interpolation threshold), it learns an inelegant, ugly explanation, one that memorizes each training point but is unhelpful out-of-sample.
Interestingly, the principle of double descent applies not just to model size, but to compute and dataset size, as well. For example, consider what happens if we start with a giant model (whose size we keep fixed) and add data to an initially-small dataset. We will start off in the overparameterized regime, and will see performance degrade (as the added data becomes hard for the model to memorize) until error reaches a peak (right at the interpolation threshold). If we then continue to add data, we will move once again into the underparameterized regime, and performance will once again improve.

A similar trend also happens when we scale compute (meaning, do more and more steps of gradient descent). Even if the model is large enough to permit a good explanation of the training data, it still may take many steps of gradient descent to find it. A similar intuition applies here as with model size. Gradient descent seems to start off by capturing high-level trends which generalize well; then, it begins to move towards models which inelegantly memorize specific train points; and finally, it settles down on a model which elegantly memorizes the train data, and by finding true patterns that generalize to out-of-sample points. In fact, we already saw this trend in action: remember this plot?
Where we were at first puzzled by the up-then-down behavior of the nonlinear regression curve, we can now recognize it as a classic example of update-wise double descent.
The core takeaway is this: you don’t need to have unbounded amounts of compute or data for deep learning to work. You just need to have enough to cross the interpolation threshold, and enter the "second descent". After that, you are free to scale up by as much as you have money to spend, and your performance will always improve.4
The Magic Of Positive Interference
What if even “enough” is asking too much? Perhaps on your task, the dataset is truly tiny, and it is prohibitively expensive to collect any more. Can deep learning still be useful? Surprisingly, the answer is still yes – or at least, a qualified maybe. The crucial piece is that you need to be able to find other data that feels related. Not the same data, not even necessarily the same task, just similar enough that it seems the two might have something in common.
Let me give you some examples to paint the picture. If you are a medical doctor, you might have only a hundred images of a particular rare cancer, but millions of pictures of non-rare cancers and healthy patients. If you are a stock trader, you might only have a hundred days of data on a recent IPO, but multiple years of data on dozens of other companies on the same stock exchange. If you are a translator, perhaps you have only a few notebook’s worth of translated sentences in a particular indigenous language, but a nearly unbounded supply of translations between languages like English and Spanish.
A common intuition is that learning to perform two tasks at once will hurt performance, relative to training on just one. But with deep learning, precisely the opposite is true – provided you have sufficient compute. The reason is that deep learning allows you to leverage this secondary source of data for feature learning. If your model is sufficiently large, and this new data really does have something in common with the task you care about, then training on both at once will allow you to learn good features from the high-data task, and leverage them for good performance on the low-data task. Don’t believe me? Let’s see it happen.
Returning to our problem, let’s now return to the setting where we have only 250 datapoints. As we saw before, even though deep learning models do come out on top of linear regression, they can somewhat overfit on this tiny dataset. But let’s say I manage to scrounge up a second dataset, containing 25,000 samples. This second dataset is for a similar task to the first one, but not the same; training on the second dataset completely fails to solve the first task. But what happens when we train a large network on both tasks together? In this plot, we always measure only the out-of-sample performance on the original task.
As you can see, adding an extra task reduces overfitting, improves generalization, and results in better overall performance. This seemingly-paradoxical outcome is incredibly common. Adding in an extra sub-task seems like it should make the problem harder, but it actually makes the problem easier. This is called “positive interference”, and it is the secret to truly impressive deep learning models like GPT-3 and its cousin, ChatGPT. By trying to learn all text on the internet in a single model, OpenAI enormously leverages positive interference between the different subtasks inherent in that goal, and winds up with a model much better at all of them than any specialist.
From another perspective, though, maybe this outcome is not so surprising. If the two tasks were incredibly similar — for example, maybe the second task is nearly the same as the first one, but with a tiny bit of noise added to some features — then it becomes obvious that combining the two tasks should help: we’ve effectively just doubled the dataset size!
More generally, it is clear that there is a smooth spectrum of task similarity, from “identical” at one end, to “completely different” at the other. When we combine the datasets of two identical tasks, it is obvious that this should improve performance on each. As we move along the spectrum, this becomes less likely to be the case, but (assuming our model is large enough) there is no point on the spectrum where combining the datasets hurts. So of course, it makes sense to combine all of our tasks into a single model, e.g. training GPT on the whole internet: since all interference is non-negative, this can only help. And, as it turns out, for that particular set of language tasks, it helps quite a lot.
Deep Learning Is (Often) Better Than Linear Regression
Okay, I exaggerated in the title. If you have really tiny data, and no data from auxiliary tasks to augment it with; or if you have severely limited budget for compute, and can’t afford to train deep learning models; if you want a model that is interpretable or auditable, rather than just being performant; or if you have a strong emotional attachment to linear regression, and would fall into a deep state of melancholy if you ever let it go; in any of these situations, you should prefer linear regression. But hopefully you can see how deep learning has a ton of potential as a drop-in replacement for linear regression. Maybe it will even be useful for your project.
Code to replicate experiments: https://github.com/jbuckman/lr-vs-dl
I want to emphasize that my experiments in this essay utilize a toy task, one designed for pedagogy, not persuasion. If you find yourself thinking, “this is an interesting experimental result but I don’t believe it will hold in general”, that’s completely reasonable! You’re right: it’s not the case that the results I show here are guaranteed to hold universally. But empirically, it does seem to be the case that these properties hold on almost every real-world task. I’m not going to compile that evidence in this essay, though; I’ll save that discussion for another day.
To avoid alienating any readers, I’m not going to tell you any more details about exactly what this task is, though full details can be found by looking at the code repository linked at the end of the essay. I tried to put together a generic-enough task that any reader can hopefully project their own goals onto it.
Actually, via clever construction, there can even be more than two. But in natural settings, as far as I’ve ever seen, there is only ever a single critical region.
There is a bit more nuance to this. Getting “enough data” is all you need to escape from the regime where you need to be worried about overfitting. But realistically, acquiring more data is also hugely important for performance; if you continue to scale model size and compute without increasing data, you will see diminishing returns. Stated concisely: once you have enough data, performance increases monotonically with scale, but the rate of improvement begins to decay.












A footnote mentions a code repository linked at the end of the essay, but I can't seem to find one. Can you provide a link?
I'm confused about the first graph (and some of the subsequent ones) - how can 1 - R^2 ever be greater than 1? Are you actually just plotting mean squared error instead?